Издержки и использование труда в производстве. Производительность труда как мера эффективности функционирования фирмы.
Экономические издержки производства товара зависят от количества используемых ресурсов и цен на услуги факторов производства. Если предприниматель использует не приобретаемые, а собственные ресурсы, цены должны быть выражены в одинаковых единицах для точного определения величины затрат. Функция издержек описывает связь между выпуском продукции и минимально возможными затратами, необходимыми для его обеспечения. Технология и цены на производственные ресурсы обычно берутся как данные при определении функции издержек. Изменение цен на какой-либо ресурс или применение улучшенной технологии отразится на величине минимальных затрат при производстве такого же объема продукции.
Неэффективное производство имеет место тогда, когда производители не могут добиться производства продукции при минимальных затратах. Из числа вариантов использования факторов производства выбирается тот, который позволяет снизить затраты, не сокращая объем выпуска продукции. С другой стороны, при неэффективном производстве производителю может быть выгодно увеличить объем выпуска продукции при имеющемся наборе ресурсов, не увеличивая затрат.
На рис.2 показана одна из изоквант для фабрики по производству стульев. Семейство изокост[1], которое соответствует заданным ценам на труд в размере 10 долларов за час и арендной плате за капитал в размере 20 долларов за час, перенесено в ту же систему координат, что и изокванта.
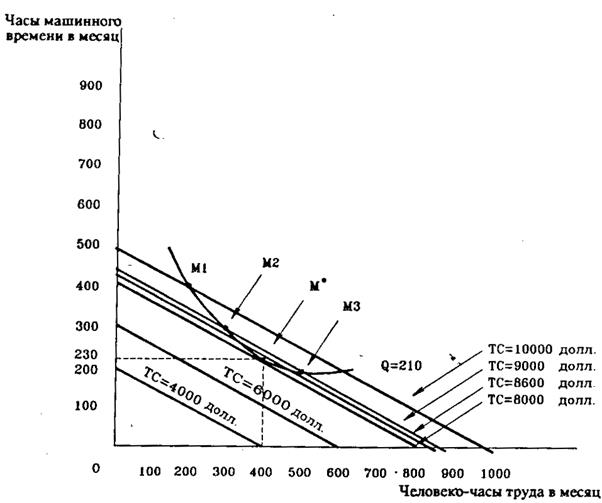
Рис.2 Минимизация издержек производства определенного объема продукции.
Функция издержек показывает связь между объемом выпуска продукции и минимальным количеством затрат, необходимых для производства этого объема продукции. Производитель стульев должен быть уверен, что при использовании данной комбинации затрат труда и капитала объем продукции будет произведен с минимальными издержками. Предположим, что владелец фабрики решил производить 210 стульев в месяц. Посмотрим на метод производства, примененный в точке М1 на изокванте. Этой точке соответствует применение 200 часов труда и 400 часов работы машин. Затраты на производство при использовании этого метода составят 10000 долларов в месяц.
Метод М2 включает применение 300 часов труда и 300 часов работы машин, а затраты составляют 9000 долларов в месяц. Метод М3 включает применение 500 часов труда и 200 часов работы машин, затраты также составят 9000 долларов в месяц. Методы М2 и М3 соответствуют точкам одной изокосты. Минимальному уровню затрат для производства 210 стульев соответствует точка М*, которая является точкой касания изокванты и изокосты. Этой точке соответствует применение 400 часов труда и 230 часов работы машин. Совокупные издержки составят 8600 долларов в месяц. Равновесный метод производства, следовательно, требует комбинации факторов в точке М*.
Условие для определения минимальных затрат производства данного объема продукции состоит в том, чтобы наклон изокванты для двух видов ресурсов был равен наклону изокосты для этих ресурсов. Наклон изокванты равен предельной норме технологического замещения трудом капитала, взятой с отрицательным знаком. Наклон бюджетной линии равен отношению цены труда к цене капитала, взятому с отрицательным знаком. Отсюда следует, что в равновесии:
MRTSLK=PL/PK (1)
Так как величину предельной нормы технологического замещения можно также представить как отношение предельного продукта труда к предельному продукту капитала, то:
MPL/MPK= PL/PK (2)
Уравнение (2) определяет условие производства любого заданного объема продукции с минимальными затратами. Фирма, если она рассчитывает вести производство согласно своей функции издержек, определяя объем производимой продукции, должна выбрать вариант такой комбинации применяемых факторов производства, чтобы выполнялось условие, приведенное выше.
Принцип наименьших затрат: равные предельные продукты факторов производства на доллар затрат.
Уравнение (2) можно записать следующим образом: